resultados, análises, expansões
discussão dos resultados
Ao analisarmos o quadro dos grafos, parece que nossa hipótese já está respondida. Nós nos perguntamos se a variação da geometria implicaria em uma variação na topologia da rede, e nossa hipótese dizia que essas seriam independentes. No quadro, fica claro que todas as geometrias apresentam as mesmas características com relação aos grafos resultantes. Quer dizer, em quaisquer das 5 geometrias tivemos a formação de redes, e também tivemos a não formação delas. Entretanto, todas as redes (com uma exceção) se formaram na distribuição aleatória das atividades, com as demais distribuições não provocando a formação de rede alguma. De uma maneira mais rígida e obtusa, poderíamos dizer que a hipótese se confirma. Mas não é isso exatamente.
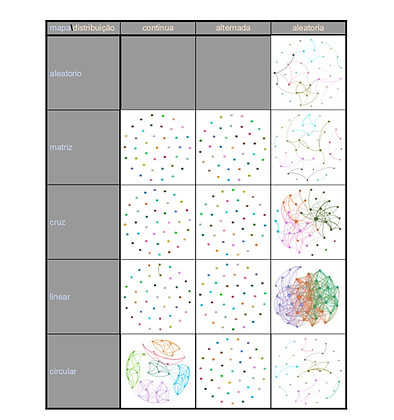
A1. resumo das topologias das cidade-redes
O caso da exceção exige uma atenção mais demorada. Como se observa, quaisquer das simulações com distribuição contínua ou alternada, independentemente da geometria do mapa, resultaram na não formação de redes, com exceção do cenário de mapa circular-contínua. Nesse caso, a rede resultante é até mais conectada no mapa circular-aleatória. Quando analisamos os vídeos das simulações, fica claro o que houve. As distribuições contínuas e alternadas acabam definindo percursos que não se cruzam, enquanto as aleatórias geram várias sobreposições. Um mapa de calor dos percursos e encontros deixaria explícito.

A2. percursos nos cenários (a) distribuição contínua (b) distribuição alternada (c) distribuição aleatória
Vale apontar que, por total liberdade de caminhar, os agentes estabelecem sempre a rota mais curta, uma linha reta. Eles esbarram entre si, mas não esbarram nas casas e trabalhos, as atravessam. Especificamente na circular-continua, todos os habitantes precisavam passar pelo centro da geometria para chegar aos seus destinos, devido à distribuição das atividades. Nesse caso, a distribuição das casas é numerada de zero até quarenta no sentido horário, e na sequência os trabalhos de zero a quarenta se distribuem na segunda metade do círculo. Isso faz com que a pessoa que está na posição zero vá para um trabalho que está a cento e oitenta graus dela, e assim por diante. O que resulta em todos os agentes se cruzarem no meio da circunferência.
No caso das distribuições alternadas, o trabalho de cada pessoa é vizinho a sua casa e desse modo os deslocamentos são tão curtos que não se sobrepõem, não criam encontros. De maneira parecida, mas talvez não exatamente igual, à distribuição contínua, que gera uma espécie de setorização. Talvez pela correspondência de sequência pessoa1 - casa1 - trabalho1, as posições relativas casa-trabalho geraram percursos paralelos, de novo sem criar qualquer oportunidade de cruzamentos e encontros.
Se, por um lado, a distribuição das atividades parece ser o componente determinante para geometrias de percurso que se cruzem, a total independência da geometria base não pode ser descartada. Temos ainda um outro ponto para analisar. As densidades das redes resultantes. Temos 3 redes com grau médio pouco abaixo de 4: circular-aleatória com 3.9, matriz-aleatória com 3.75 e a aleatória com 3.8. Depois temos a cruz-aleatória com 7.1, a nossa exceção circular-contínua com 11.25 e a linear-aleatória com maior densidade, um grau médio de 19.2. Esses patamares ficam mais evidenciados ainda no número de cliques ou triângulos de cada uma, como na tabela A3.

A3. resumo redes organizadas por grau
Se olharmos para a geometria dos percursos, podemos perceber o seguinte: nas três redes com menor densidade - aleatória, em matriz e circular - os caminhos estão dispersos por uma área maior, havendo sobreposição e encontros em toda ela.
No caso da distribuição em cruz, a própria geometria induz uma limitação da área para os percursos, restringindo a região de sobreposição e encontros. A restrição dessa área de movimento e encontros é ainda mais evidente na rede linear, onde praticamente não há espaço de liberdade para o deslocamento. Nesse caso, todos os caminhos se sobrepõem na área bastante restrita da linha, levando a encontros frequentes devido a essa restrição espacial.
A rede circular contínua é um caso diferente. A área “disponível” para os percursos é a mesma que nos demais mapas circulares. Mas, devido à especificidade da distribuição de os pares casa-trabalho estarem em lados opostos, todos os agentes precisam passar pelo centro, criando uma área de sobreposição de percursos bastante densa onde ocorrem todos os encontros.
Esses casos nos mostram que a área total ocupada pela geometria tende a influir na densidade final da rede de encontros ao restringir a geometria dos percursos, aumentando as suas sobreposições e daí os encontros. Entretanto, isso não é suficiente. É a distribuição dos pontos de origem-destino que é fundamental. Ao final, a influência da geometria do mapa está na maneira como ela pode delimitar as regiões de encontro.
Outra questão, que fica em aberto, é a relação entre a rede formada e a distribuição das atividades. Apontamos que as redes observadas são todas aleatórias assim como a distribuição das atividades, com exceção para o mapa circular-contínuo. Isto pode sugerir uma correlação entre elas. Ao mesmo tempo, o caso do mapa circular-contínuo se coloca como evidência contrária. Uma nova investigação seria necessária para verificar se a topologia da cidade-rede segue a topologia dessa distribuição das origens e destinos. Por exemplo, caso a distribuição das atividades siga alguma outra lógica espacial, como uma associação preferencial ou qualquer padrão de preferência, se isso se refletirá na topologia da cidade-rede. Portanto, em um momento posterior, seria interessante investigar não mais se é a geometria da cidade-física que interfere, mas se é a lógica de espacialização das atividades e, consequentemente, a geometria resultante desses percursos. Imaginamos que esses elementos estejam diretamente associados à topologia final da rede. São, entretanto, questões para estudos futuros.
síntese
O simulador Redinha, como ferramenta para prova de conceito, se mostrou bastante eficaz. Como previsto, os programas de computador são boas ferramentas para explorar axiomas e hipóteses por só incluírem as discussões que foram codificadas e permitirem explorar as consequências limite delas. Por ventura da decisão inicial de se simular também diferentes distribuições das atividades, se pôde observar como essa é a variável mais relevante para a rede de encontros formada. Ao mesmo tempo, o estudo dos resultados mostrou que seria importante ter outras métricas, como mapa de calor dos percursos e encontros dos agentes, área da geometria geral, e área do polígono de encontros pelo menos. Outras métricas certamente podem ajudar a esclarecer questões como as influências da geometria do mapa com relação a área de encontros resultante, correlação entre geometria de ocupação do território com a topologia das redes e geometria dos percursos, entre outros. São outras dimensões e axiomas que precisariam ser codificadas para teste.
Com relação à nossa hipótese, encontramos que a geometria subjacente da cidade-física apenas interfere na topologia da cidade-rede resultante na medida em que delimita regiões de sobreposição de percursos, onde podem acontecer os encontros. A topologia da rede é provocada pela geometria dos percursos a partir das sobreposições entre os percursos dos agentes e a probabilidade do encontro consequente. A geometria dos percursos é determinada pela distribuição espacial das atividades. Se essas duas topologias são equivalentes, precisa ainda de estudo para esclarecimento.