resultados, análises, expansões
— De agora em diante, começarei a descrever as cidades — dissera Khan. — Nas
suas viagens, você verificará se elas existem.
Mas as cidades visitadas por Marco Polo eram sempre diferentes das imaginadas
pelo imperador.
— Entretanto, construí na minha mente um modelo de cidade do qual extrair todas
as cidades possíveis — disse Kublai. — Ele contém tudo o que vai de acordo com as
normas. Uma vez que as cidades que existem se afastam da norma em diferentes graus,
basta prever as exceções à regra e calcular as combinações mais prováveis.
— Eu também imaginei um modelo de cidade do qual extraio todas as outras —
respondeu Marco. — É uma cidade feita só de exceções, impedimentos, contradições,
incongruências, contrassensos. Se uma cidade assim é o que há de mais improvável,
diminuindo o número dos elementos anormais aumenta a probabilidade de que a
cidade realmente exista. Portanto, basta subtrair as exceções ao meu modelo e em
qualquer direção que eu vá sempre me encontrarei diante de uma cidade que, apesar
de sempre por causa das exceções, existe. Mas não posso conduzir a minha operação
além de um certo limite: obteria cidades verossímeis demais para serem verdadeiras.
as cidades invisíveis, p 67
resultados
O simulador de geometria-rede Redinha foi desenvolvido considerando a simulação do dia a dia de uma determinada população na sua comutação casa-trabalho por um determinado número de ciclos. O objetivo era observar e comparar as redes de encontros resultantes da simulação em cenários com “cidades” de diferentes geometrias.
Para tanto, em um mapa base, foram geradas geometrias sobre as quais foram marcados lugares, para em seguida serem atribuídos o uso de casa ou trabalho. Na sequência, cada agente (pessoa) foi associado a um par casa-trabalho. As geometrias foram escolhidas de maneira arbitrária mas buscando o máximo de diferença topológica entre elas. Os lugares foram localizados ao longo de 5 formas: círculo, cruz, linha, matriz, e pontos aleatórios no mapa.
Após isso, o uso de casa ou de trabalho foram distribuídos de três maneiras: contínua, alternada e aleatória. Essas duas primeiras distribuições foram pensadas como algum paralelo em relação ao modelo setorizado modernista e a ideia de unidades de vizinhança ou mesmo o plano isotrópico, respectivamente. Cada par casa-trabalho foi vinculado a um agente. Essa configuração elimina o impacto do acúmulo de pessoas numa atividade na formação de rede, permitindo observar só a influência da geometria. Definida a distribuição no mapa, os agentes têm liberdade total de movimento buscando o caminho mais curto, resultando em percursos sempre em linha reta, embora eventualmente esbarrando uns nos outros. Devido a limitações de poder de processamento, foram utilizados 40 agentes, sem prejuízo do estudo que se buscava. Todas elas rodaram 10 ciclos, simulando 10 dias. O objetivo foi estabelecer a rede de encontro, e eventualmente alguma métrica de quais agentes passam mais tempo juntos, traduzida no valor do peso da aresta.
R1. resultados das simulações e análises no Gephy

Com a combinação entre as 5 geometrias e as 3 maneiras de distribuição, foram produzidos 13 mapas (figura R1). A redundância resultante da variação da distribuição sobre o mapa aleatório implicou em apenas 1 mapa aleatório. Para cada cenário foi simulada uma rotina de comutação casa-trabalho de 10 dias, produzindo uma matriz com os encontros que aconteciam. Essa matriz foi analisada no software de análise de redes Gephy. Como resultado da análise, o programa retornou um grafo topológico da rede, bem como uma série de propriedades, incluindo índice de clusterização, grau dos nós, diâmetro e densidade. Esses resultados rede a rede estão disponíveis nos links respectivos no quadro R1, e sumarizados no quadro R2 abaixo.
R2. retorno Gephy
Deste quadro R2, os parâmetros mais relevantes para a diferenciação que usamos são: o grau, que indica o número médio de conexões dos nós; o diâmetro e o comprimento médio de caminho, que são proporcionais ao número de ciclos para propagação de informação; o número de comunidades, que indica a quantidade de clusters; o número de componentes conectados, que indica em quantos conjuntos os nós estão agrupados, e o número de triângulos, ou cliques, que indica o grau de interconexão entre os nós. Para efeito de visualização no Gephy, foi adicionado 1 na diagonal da matriz de conexões, criando a aresta pii, o que implicou grau 2 nos casos em que não se estabeleceu nenhuma conexão entre os agentes, significando a ligação dele com ele mesmo. Para os demais parâmetros, essa aresta fica diluída. Além disso, só nos interessa uma ordem de valor e não fizemos nenhuma medida em cima do peso das arestas, de modo que a sensibilidade para o nosso interesse não fica afetada.
mapa aleatório
Este mapa formou 14 componentes distintos (connected components) com 18 comunidades. Foram 10 formados por agentes que não encontraram ninguém, 2 grupos com 2 nós, 1 com 3, e outro grupo com os demais 23 elementos (size distribution do connected components report). Dentre as comunidades, os maiores clusters reuniram 6 agentes (size distribution do modularity report), 1 clusters com 5, 1 com 4, outro com 2 e 3 clusters com 2 agentes. Na rede foram formados 16 triângulos. O seu diâmetro máximo é de 10 arestas, com um caminho médio de 3,87.
mapa matriz.distribuição contínua
Este mapa não formou nenhuma conexão, mantendo-se os 40 agentes isolados.
mapa matriz.distribuição alternada
Este mapa não formou nenhuma conexão, mantendo-se os 40 agentes isolados.
mapa matriz.distribuição aleatória
Este mapa formou 9 componentes distintos (connected components) com 12 comunidades. Foram 5 formados por agentes que não encontraram ninguém, 2 grupos com 2 nós, 1 com 6, e outro grupo com os demais 25 elementos (size distribution do connected components report). Dentre as comunidades, o maior cluster reuniu 10 agentes (size distribution do modularity report), 2 clusters com 6, 1 com 5, outro com 4 e 2 clusters com 3 agentes. Na rede foram formados 11 triângulos. O seu diâmetro máximo é de 11 arestas, com um caminho médio de 4,14.
mapa cruz.distribuição contínua
Este mapa não formou nenhuma conexão, mantendo-se os 40 agentes isolados.
mapa cruz.distribuição alternada
Este mapa não formou nenhuma conexão, mantendo-se os 40 agentes isolados.
mapa cruz.distribuição aleatória
Este mapa formou 4 componentes distintos (connected components) com 7 comunidades. Foram 3 formados por agentes que não encontraram ninguém e um outro grupo com os demais 37 elementos (size distribution do connected components report). Dentre as comunidades, o maior cluster reuniu 16 agentes (size distribution do modularity report), 1 clusters com 14, 1 com 4, e outro com 3. Na rede foram formados 87 triângulos. O seu diâmetro máximo é de 6 arestas, com um caminho médio de 2,30.
mapa linha.distribuição contínua
Este mapa formou a conexão entre apenas 2 agentes, mantendo-se os demais 38 isolados.
mapa linha.distribuição alternada
Este mapa não formou nenhuma conexão, mantendo-se os 40 agentes isolados.
mapa linha.distribuição aleatória
Este mapa formou apenas 1 componente (connected components) conectando todos os agentes (size distribution do connected components report), com 2 comunidades, uma reunindo 22 dos nós e a outra os 18 restantes (size distribution do modularity report). Na rede foram formados 1203 triângulos. O seu diâmetro máximo é de 3 arestas, com um caminho médio de 1,60.
mapa circular.distribuição contínua
Este mapa formou apenas 1 componente (connected components) conectando todos os agentes (size distribution do connected components report), com 6 comunidades. A maior delas reuniu 10 nós, e as outras 5 reunindo 8, 7, 6, 5, 4 agentes (size distribution do modularity report). Na rede foram formados 459 triângulos. O seu diâmetro máximo é de 5 arestas, com um caminho médio de 2,56.
mapa circular.distribuição alternada
Este mapa não formou nenhuma conexão, mantendo-se os 40 agentes isolados.
mapa circular.distribuição aleatória
Este mapa formou 11 componentes distintos (connected components) com 15 comunidades. Foram 7 formados por agentes que não encontraram ninguém, 2 componentes formados por 2 agentes, 1 reunindo 4 e um outro grupo com os demais 25 elementos (size distribution do connected components report). Dentre as comunidades, os 2 maiores clusters reuniram 7 agentes (size distribution do modularity report), 1 clusters com 5, outro com 4, 2 com 3 e 2 clusters com 2 agentes. Na rede foram formados 15 triângulos. O seu diâmetro máximo é de 8 arestas, com um caminho médio de 3,48.
Os resultados dos grafos dos 13 mapas gerados, sintetizados no Quadro R1 e resumidas no quadro R3, oferecem um resumo visual de fácil leitura. A primeira coisa evidenciada é que 6 cenários formam rede, e os demais 7, não. Também fica claro que, em todo cenário com distribuição aleatória de casas e trabalhos, houve formação de rede. Em nenhum dos outros cenários, houve formação de alguma rede, com exceção do mapa com geometria circular e distribuição contínua.
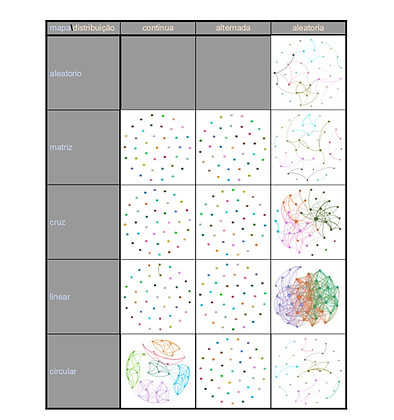
R3. topologias das redes formadas
As redes formadas apresentam intensidade de conectividade diferente, e sempre com a presença de clusters. Nenhuma delas, entretanto, apresenta distribuição regular quanto ao grau, e tão pouco alguma conexão preferencial. A própria natureza da distribuição das funções sugere uma rede de formação aleatória. A distribuição do grau dessas redes apresenta uma tendência de distribuição normal (R4), o que deve ficar mais claro num cenário com um número maior de agentes.

R4. distribuição de grau



















